Нечёткая логика и теория нечётких множеств
Это раздел математики, являющийся обобщением классической логики и теории множеств. Понятие нечёткой логики было впервые введено профессором Лютфи Заде в 1965 году. В этой статье понятие множества было расширено допущением, что функция принадлежности элемента к множеству может принимать любые значения в интервале [0...1], а не только 0 или 1. Такие множества были названы нечёткими. Также автором были предложены различные логические операции над нечёткими множествами и предложено понятие лингвистической переменной, в качестве значений которой выступают нечёткие множества.
Содержание |
Математические основы
Символическая нечёткая логика
Символическая нечёткая логика основывается на понятии t-нормы. После выбора некоторой t-нормы (а её можно ввести несколькими разными способами) появляется возможность определить основные операции над пропозициональными переменными: конъюнкцию, дизъюнкцию, импликацию, отрицание и другие. Нетрудно доказать теорему о том, что дистрибутивность, присутствующая в классической логике, выполняется только в случае, когда в качестве t-нормы выбирается t-норма Гёделя. Кроме того, в силу определенных причин, в качестве импликации чаще всего выбирают операцию, называемую residium (она, вообще говоря, также зависит от выбора t-нормы). Определение основных операций, перечисленных выше, приводит к формальному определению базисной нечёткой логики, которая имеет много общего с классической булевозначной логикой (точнее, с исчислением высказываний). Существуют три основных базисных нечётких логики: логика Лукасевича, логика Гёделя и вероятностная логика (англ. product logic). Интересно, что объединение любых двух из трёх перечисленных выше логик приводит к классической булевозначной логике.
Теория приближенных вычислений
Основное понятие нечёткой логики в широком смысле - нечёткое множество, определяемое при помощи обобщенного понятия характеристической функции. Затем вводятся понятия объединения, пересечения и дополнения множеств (через характеристическую функцию; задать можно различными способами), понятие нечёткого отношения, а также одно из важнейших понятий - понятие лингвистической переменной. Вообще говоря, даже такой минимальный набор определений позволяет использовать нечёткую логику в некоторых приложениях, для большинства же необходимо задать ещё и правило вывода (и оператор импликации).
Нечеткая логика и нейронные сети
Поскольку нечеткие множества описываются функциями принадлежности, а t-нормы и k-нормы обычными математическими операциями, можно представить нечеткие логические рассуждения в виде нейронной сети. Для этого функции принадлежности надо интерпретировать как функции активации нейронов, передачу сигналов как связи, а логические t-нормы и t-конормы, как специальные виды нейронов, выполняющие математические соответствующие операции. Существует большое разнообразие подобных "нейро-фаззи" сетей neuro-fuzzy network (англ.). Например, ANFIS (Adaptive Neuro fuzzy Inference System) - адаптивная нейро-фаззи система вывода , она может быть описана в универсальной форме аппроксиматоров как
Примеры
Нечёткое множество, содержащее число 5 Нечёткое множество, содержащее число 5, можно задать, например, такой характеристической функцией:
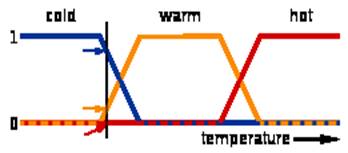
Пример определения лингвистической переменной
В обозначениях, принятых для лингвистической переменной (рис.1):
X = «Температура в комнате»
U = [5, 35]
T = {"холодно", «комфортно», «жарко»}
Характеристические функции:
Правило G порождает новые термы с использованием союзов «и», «или», «не», «очень», «более или менее».
- не A:
- очень A:
- более или менее A:
- A или B:
- A и B: